risk = nil;

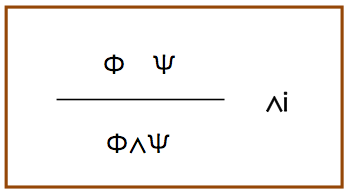
更に，自然演繹における推論規則 ¹を見ていく．最初は，連言である．

入-∧

右側にある∧iは，この推論規則の名前である．図のタイトルは筧先生に敬意を表してプログラミングの科学にある名前をつけている．意味は明らかで，Φが真と分かり，ψも真と分かった．このとき，Φ∧Ψも真である．規則として名前付けをしておく．連言記号を挿入しているので，入-∧という名前になっている（英語は，introductionの先頭文字である）．

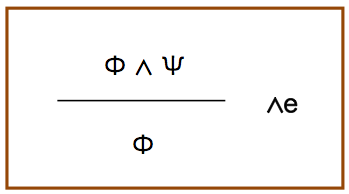
次は，逆のパターンである．

去-∧

こちらは，連言記号をとることができるという規則である．Φ∧ψが真という前提ならば，Φは当然真でなくてはならない．結論は，ψでも同じである．英語の名称は，eliminationから来ている．

いま，次を考える．

p∧q, r ⊢ q∧r

p∧qに対して，∧e規則を適用すると，qが出てくる．前提は，q, r と変形できるので，∧i規則を適用して，q∧rと結論づけることができる．ということで上記は正しいことが分かる．

前回と同様に単純な規則を順次適用することで，結論が正しいことを示すことができる．

(nil)