risk = nil;

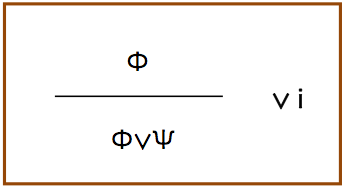
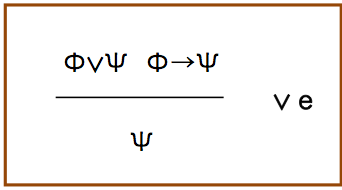
次は選言がある場合の推論規則である．

入 -∨

これは，見るからに興味深い．前提が真であれば，結論が真であることは見て取れる（もちろん前提は，Ψでも同じである）．従って妥当な推論であるが，違和感が残る．

いま，Φ「雨が降っている」とし，Ψ「隕石が落下している」とすると，雨が降っているという前提から，「雨が降っているか隕石が落下している」という結論が得られる．あくまで推論の規則であると割り切る．

次は，ちょっと複雑な例である．機械的な適用しやすさを考えるときに，採用しない場合もある．

去- ∨

結論を否定すると，前提の前半部分からΦが真である必要がでてくる．そうすると次のΦ→ψが成立しなくなるので，結論は正しいということになる．

どのような推論規則を使うと効率よく，推論（証明）ができるかには，幾つかの流儀がある．タブローという方法もまた，その手段の一つである．多くの教科書で説明があるので，ここでは省略する ¹．

(nil)