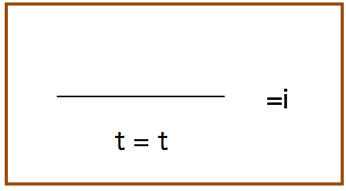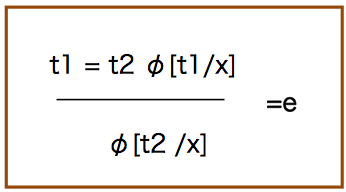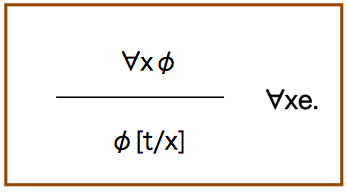さて，今回は述語論理における推論（証明）規則である．
最初の規則である．
入-=
これは，当たり前で，かつ余り役に立たない．次は，等号に関する削除の規則である．
去-=
いま，xがΦの束縛変数とする．明らかにt1, t2 は自由変数となる．t1 と t2 は等しいので，Φ[t2/x]と結論づけることができる．少し具体的な例を見てみる．それぞれ論理式は以下だとする．
t1: (x+1)
t2: (1+x)
Φx:((x>1)→(x>0))
論理式Φ[t1/x] は，（(x+1)>1)→((x+1)>0)である（t1/xは置き換えを表す）．いま，t2に変えた論理式 ((1+x)>1)→((1+x)>0)も正しいことがわかる．
さて，このどこが述語論理式の推論規則かと思ってしまうが，次につながる．
instantiation
インスタンス化（instantiation）と呼ばれる述語論理の推論規則を得ることができる．
前提が示すところは，全ての束縛変数xに関してΦは成立している．だとすると，例えば定項としてt（変項xの一つの値）をいれた場合でも成立しなくてはならない．
ずいぶんと後退しているようであるが，全称限量子を外せる効果は大きい．
(nil)