さて,前回は,手計算で重みとCIを手計算で行った.実際に手計算することはないと思うが,一度だけなら楽しい.
さて,前回のペア比較は,ソフトを改修した場合の効果についてのものだったとする.代替案A>代替案C>代替案Bの順番であったから,代替案Aが最も効果的ということになる.次は費用に関して同様に計算してみる(今回は手計算しない).
| 代替案A | 代替案B | 代替案C | |
| 代替案A | 1 | 1/4 | 1/5 |
| 代替案B | 4 | 1 | 1/2 |
| 代替案C | 5 | 2 | 1 |
重みベクトルとCIは,次になる.
[0.097, 0.333, 0.570]t , CI = 0.012
CIは,0.1より小さいので有効である.さて,費用から見た場合の代替案の重要度は,代替案C>代替案B>代替案Aとなる.これは,効果から見た場合の優先度とは異なっている.最終的に,どのような優先度とすべきか.
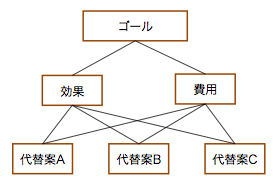
AHPは,その名前の通り階層構造をとる.ゴールをレベル1,効果と費用をレベル2,各代替案をレベル3とすると,レベル2とレベル3の間の重み付けは既に計算している.以下の結果であった(ここでは,有効桁数を増やした結果を示す).
[0.743, 0.063, 0.194]t
次に,レベル1とレベル2の間の重み付けを考える.これまでと同様に,ペア比較表を作る.
| 効果 | 費用 | |
| 効果 | 1 | 1/5 |
| 費用 | 5 | 1 |
いまは,とにかく費用を重視したいとする.ここから計算する重み付けは,以下になる.
[0.167, 0.833]t
最終的な,重み付けは,それぞれの積和をとることで計算できる.費用対効果を勘案した,代替案の重みは,次になる.
代替案A:0.167 * 0.743 (効果分)+ 0.833 * 0.097 (費用分)= 0.205
代替案B:0.167 * 0.063 (効果分)+ 0.833 * 0.333 (費用分)= 0.288
代替案C:0.167 * 0.194 (効果分)+ 0.833 * 0.570 (費用分)= 0.507
従って,最終的な代替案の評価は,代替案C>代替案B>代替案Aとなる.「効果」に比べ,今回は「費用」をかなり重視したので,費用単独の順位と同じになっている.ちなみに,KAOSの教科書では,効果と費用は同一の重みで比較している.
さて,AHPについて,少し詳しく見てきた.少し前のAHPの本[ref]木下栄蔵,AHPの理論と実際, 2000[/ref]では,様々なヴァリエーションの説明がある.相対的な評価ではなく絶対的な評価を行うもの,必ずしも独立性を前提としないものなどである.構造も単純な木構造ではなく,ネットワーク型となるものもある.
何度かこの項で説明しているように,ある種の合理的な説明は,これからも必要だろうと思う.そのときに,(最も基本的なモデルにおいても)AHPは,良い計算手段を提供している.
(nil)