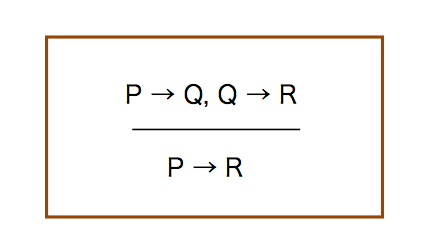今回は推論（導出）規則である．或いは，論証のパターンとも呼ばれる．なお，論証といっても，命題論理の範疇であって，日常生活で我々が常にそうしているというわけではない（多足，トゥールミン）
推論規則としては，自然演繹に基づく基本的な推論規則をまず示すべきであるが，先ずはここでは原書に合わせる．Resolutionと呼ばれるものを示す（基本的な推論規則と異なっているわけではない）．今も人工知能という言葉は，クラウドや自動車の支援システムとともに復活した感があるが，その少し前の時代に人気があったときの基本となるアプローチである．
modus ponens
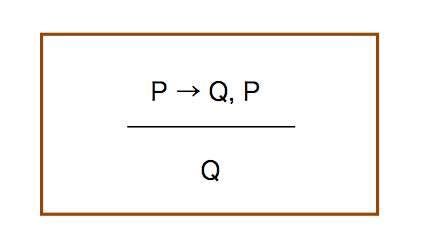
分子にあたる部分（上段）が前提であり，分母にあたる部分が結論である．
上段の意味は次になる：P→Qが成り立ち，いまPが真だとする．このとき，Qが成り立つ．
モーダスポネンス(modus ponens)といういわゆる肯定式である．よく知られている推論で，小学生でも知っていると思う．ただ，これだけだと余りありがたみを感じない．「今日飲んでくるなら，ごはんはいらないね」という文は，P：「飲んでくる」→Q：「ごはんはいらない」と考えられるが，日常生活において，通常はPが真であることを含んでいる．Pが真かどうかが全くの不明なときには，発話されない．従って，文の意義としては，「のみにいけなくておなかをすかして帰ってきても，食べるものはないと思え」ということである．条件文を伝えたいわけではない．まして，本当に飲んできたときに（Pが真），ご飯がない（Qが真）ことにあらためて感心したいわけでもない．
語用論的世界の例は，あんまりかもしれないが，会話でなくても同じである．そのことについては，書く機会もあると思う．
ちなみに，分数方式ではない別の（フレーゲ風の?）記述法もある．
P → Q, P ⊢ Q
こちらは，場所をとらない．しかし，基本は分数方式で書くことにする．
同様に，別の推論規則を見る．推移律（transitive law）とも呼ばれる．
chaining
PならばQで，QならばRから，PならばRである．
いわゆる「風が吹けば」文である．ゼロとイチの世界だから成立する．
resolution
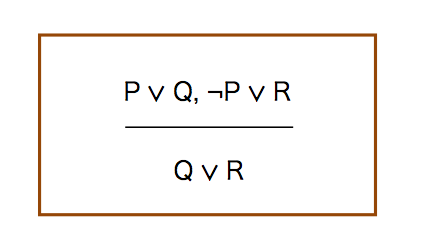
複雑に見えるが，まず，P ∨ Qが成り立っている．かつ，¬P ∨ Rも成り立っている．いま，Pが偽のときには，Qが真である必要がある．逆に，Pが真のときには，Rが真でなければならない．従って，Q ∨ Rとなり，Pを取り除くことができる．
いま，次が成り立っているとする．
¬trainMoving ∨ doorsClosed, trainStopped ∨ trainMoving
これは，resolutionの規則によって次になる（trainMovingの位置が異なっているので注意）．
doorsClosed ∨ trainStopped
これらは，複雑な命題式を簡略化するために用いる．上記に上げた３つの例とも，原子式がひとつ減っているのに気づく．一つしか減らないが，繰り返して適用することができれば，複雑な式も最終的には簡単な答えを得ることができる．機械的に解くための方法である．
