次は選言がある場合の推論規則である.
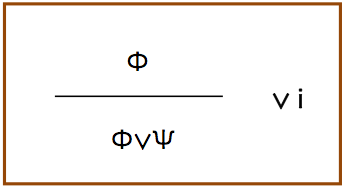
入 -∨
これは,見るからに興味深い.前提が真であれば,結論が真であることは見て取れる(もちろん前提は,Ψでも同じである).従って妥当な推論であるが,違和感が残る.
いま,Φ「雨が降っている」とし,Ψ「隕石が落下している」とすると,雨が降っているという前提から,「雨が降っているか隕石が落下している」という結論が得られる.あくまで推論の規則であると割り切る.
次は,ちょっと複雑な例である.機械的な適用しやすさを考えるときに,採用しない場合もある.
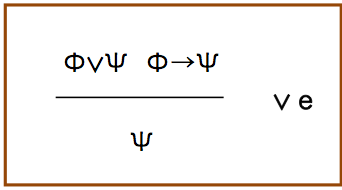
去- ∨
結論を否定すると,前提の前半部分からΦが真である必要がでてくる.そうすると次のΦ→ψが成立しなくなるので,結論は正しいということになる.
どのような推論規則を使うと効率よく,推論(証明)ができるかには,幾つかの流儀がある.タブローという方法もまた,その手段の一つである.多くの教科書で説明があるので,ここでは省略する .
(nil)
引き続き,推論規則である.最初の例は,以前に出てきた.
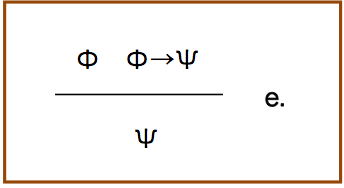
modus ponens
原子式の記号が,ギリシャ文字に変わっているが同じである.Φが削除されているので,ここでは単に「e.」規則としている.日本語方式だと,「去-→」である.
ちなみに,「入->」というのは何であろうか.これまで使ってきた演繹そのものを指す.Φ,Ψが真ならばΞであるというときに,Φ,Ψ→Ξ が結論になるような推論規則である.
上記は,modus ponens という名前を持つ.これはラテン語で,肯定の方法という意味とのこと(動詞原形のponoは「置く」,tolloは「持ち上げる」というのが基本的な語義だと思う).結論が肯定なのでこの名前がある.否定の方法(modus tollens)というのもあり,以下の形になる.
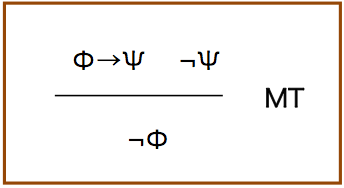
modus tollens
先と同様に原子式ψが消える.かつ結論は,否定の形式になっている.
真理値表を使って,Φ→Ψが真で,後件が偽の場合というのは前提Φが偽の場合しかないことから分かる(Φが偽だと,Ψの値によらず真になる).或いは,¬Φ ∨ Ψという変形を用いて,¬Ψが真であることから導いても良い.
では,次はどうであろうか.
Φ → Ψ , ¬Φ ⊢ ¬Ψ
前件の否定(Denying the antecedent)と呼ばれる.もちろん正当ではない.「Φ → Ψ」において,前件が偽であれば,後件は真偽の何れでも取り得る.
ここで,→について少し考えてみる.
含意
| Φ |
ψ |
Φ→ψ |
| 1 |
1 |
1 |
| 1 |
0 |
0 |
| 0 |
1 |
1 |
| 0 |
0 |
1 |
Φ:「雨が降る」
Ψ:「スリップしやすくなる」
このとき,「Φ→Ψ」だとすると,雨が降っていないときには,Ψの真偽によらずに,この式が真になるというのは,どういうことだろうか.
日常会話で,「雨が降っているとスリップしやすいよね」というときに,雨が降っていないときのことを気にしていないか,(相対的に)スリップしにくいと考えている.プログラムに対応させると次にようになるかもしれない.
Φが偽の場合は,そもそもΨは評価対象ではない.
一様の表だが,前件部が偽の場合を考えると,自然言語とプログラムとも異なっていることが分かる.そういうシンボルの体系だということである.
(nil)
推論(証明)規則の続きである.
¬¬e: ¬¬Φ ⊢ Φ
いま考えている論理では,2つの値しかとらないとする.従って,否定を重ねる(¬が2つ)ことで元に戻る(¬がゼロ).¬¬e規則(去-¬)と呼ばれる.
次は加える規則である.¬¬i規則(入-¬,が日本語バージョン.先と同様に¬の数が1つか2つかの違いがあるが,名称が異なるだけで,操作としては同じである).
¬¬i:Φ ⊢ ¬¬Φ
次の日本語の文を考える.
雨が降っていないというのは真ではない.
¬¬e規則を適用すると二つの否定を取り除くことになるので,次のようになる.
雨が降っている(というのは真である).
明快さは後者だが,前者からは微妙に降っている雨の様子が想像できるのに対して,後者は程度について分からない.しかし,その日本語としての読み込みはしないというのが,前提である.また,間違いを避けるためにも,要求書中の文中では,二重否定は望ましくない.
今回も例題である.
次は正しいか.
p, ¬¬(q∧r) ⊢ ¬¬p ∧ r
前提は,¬¬eと,前回の∧i規則によって,p ∧(q∧r)となる.q∧rは,∧e規則によって,rとできる.pに対して,更に¬¬iを適用すれば,¬¬p ∧ rとなる.
(nil)



