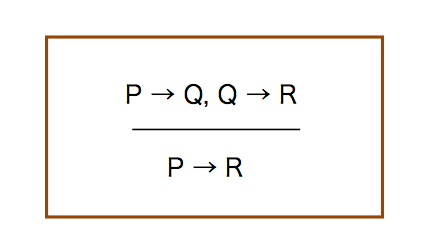更に,自然演繹における推論規則 を見ていく.最初は,連言である.
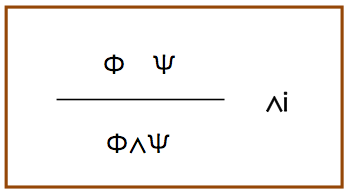
入-∧
右側にある∧iは,この推論規則の名前である.図のタイトルは筧先生に敬意を表してプログラミングの科学にある名前をつけている.意味は明らかで,Φが真と分かり,ψも真と分かった.このとき,Φ∧Ψも真である.規則として名前付けをしておく.連言記号を挿入しているので,入-∧という名前になっている(英語は,introductionの先頭文字である).
次は,逆のパターンである.
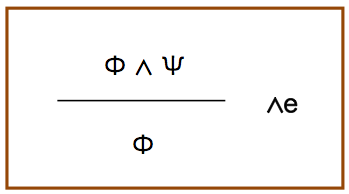
去-∧
こちらは,連言記号をとることができるという規則である.Φ∧ψが真という前提ならば,Φは当然真でなくてはならない.結論は,ψでも同じである.英語の名称は,eliminationから来ている.
いま,次を考える.
p∧q, r ⊢ q∧r
p∧qに対して,∧e規則を適用すると,qが出てくる.前提は,q, r と変形できるので,∧i規則を適用して,q∧rと結論づけることができる.ということで上記は正しいことが分かる.
前回と同様に単純な規則を順次適用することで,結論が正しいことを示すことができる.
(nil)
今回は推論(導出)規則である.或いは,論証のパターンとも呼ばれる.なお,論証といっても,命題論理の範疇であって,日常生活で我々が常にそうしているというわけではない(多足,トゥールミン)
推論規則としては,自然演繹に基づく基本的な推論規則をまず示すべきであるが,先ずはここでは原書に合わせる.Resolutionと呼ばれるものを示す(基本的な推論規則と異なっているわけではない).今も人工知能という言葉は,クラウドや自動車の支援システムとともに復活した感があるが,その少し前の時代に人気があったときの基本となるアプローチである.
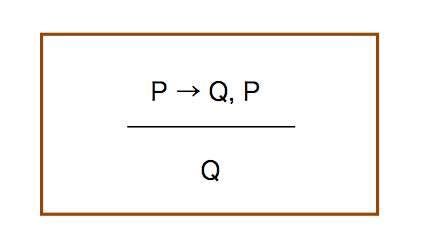
modus ponens
分子にあたる部分(上段)が前提であり,分母にあたる部分が結論である.
上段の意味は次になる:P→Qが成り立ち,いまPが真だとする.このとき,Qが成り立つ.
モーダスポネンス(modus ponens)といういわゆる肯定式である.よく知られている推論で,小学生でも知っていると思う.ただ,これだけだと余りありがたみを感じない.「今日飲んでくるなら,ごはんはいらないね」という文は,P:「飲んでくる」→Q:「ごはんはいらない」と考えられるが,日常生活において,通常はPが真であることを含んでいる.Pが真かどうかが全くの不明なときには,発話されない.従って,文の意義としては,「のみにいけなくておなかをすかして帰ってきても,食べるものはないと思え」ということである.条件文を伝えたいわけではない.まして,本当に飲んできたときに(Pが真),ご飯がない(Qが真)ことにあらためて感心したいわけでもない.
語用論的世界の例は,あんまりかもしれないが,会話でなくても同じである.そのことについては,書く機会もあると思う.
ちなみに,分数方式ではない別の(フレーゲ風の?)記述法もある.
P → Q, P ⊢ Q
こちらは,場所をとらない.しかし,基本は分数方式で書くことにする.
同様に,別の推論規則を見る.推移律(transitive law)とも呼ばれる.
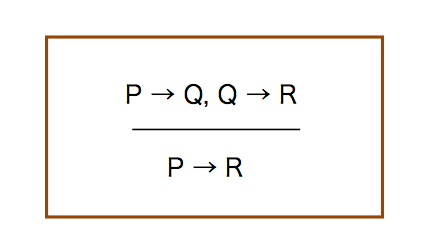
chaining
PならばQで,QならばRから,PならばRである.
いわゆる「風が吹けば」文である.ゼロとイチの世界だから成立する.
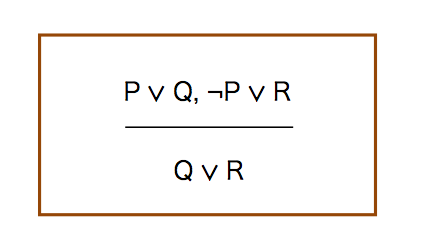
resolution
複雑に見えるが,まず,P ∨ Qが成り立っている.かつ,¬P ∨ Rも成り立っている.いま,Pが偽のときには,Qが真である必要がある.逆に,Pが真のときには,Rが真でなければならない.従って,Q ∨ Rとなり,Pを取り除くことができる.
いま,次が成り立っているとする.
¬trainMoving ∨ doorsClosed, trainStopped ∨ trainMoving
これは,resolutionの規則によって次になる(trainMovingの位置が異なっているので注意).
doorsClosed ∨ trainStopped
これらは,複雑な命題式を簡略化するために用いる.上記に上げた3つの例とも,原子式がひとつ減っているのに気づく.一つしか減らないが,繰り返して適用することができれば,複雑な式も最終的には簡単な答えを得ることができる.機械的に解くための方法である.
(nil)
論理は,他の形式的なシステムと同様に,次の3つのコンポーネントから成り立っている.構文・意味・証明論である(p.146)
-
構文は,文法に合った文を定義するための一連の規則である
-
意味は,文の正確な意味を定義するための一連の規則である
-
証明は,既存の文から新しい文を導出するための,一連の導出規則 である.
命題論理
最初の例は,以下である.
trainMoving → doorsClosed
多くの人は,「列車が動いているならば,ドアは閉まっている」と考えるに違いない.文の魅力は「省略」にあると思っているが(俳句が典型的な例),それは人が読み取ろうとする力を惹起するからと思っている.
さて,4.4節は,基本的に原書に従うが,規則中心にはしないつもりである.論理学の日本語の教科書としては,「論理学をつくる」というすばらしい入門書がある .「つくる」ということばがとても良い.あるいは,D.グリースの「プログラミングの科学」がある .
さて,命題論理では,trainMoving を以下に変えても全く差し支えがない.即ち,命題論理の世界では,原子式(単純命題)の中身を読み取ってはいけない.
- 列車は動いている,
- P
- trainStopped
記号の中身は問わない.∧(かつ)や ∨(または)といった演算子による記号の操作である.現実の我々の考え方に関係はしているが,基礎づけられているわけではない.似ている点があったとしても,現実世界とは別に成立しているのである.分かりづらさがあるとすれば,どっちつかずに見える点かもしれない.
先の式は,よく知られているように次のように変形できる.
¬trainMoving ∨ doorsClosed
→(含意,条件法)は,扱いにくいので,この変形が行われる.最初だけ真理値表で確認しておこう.
真理値表
| P |
Q |
P→Q |
¬P |
¬P∨Q |
| T |
T |
T |
F |
T |
| T |
F |
F |
F |
F |
| F |
T |
T |
T |
T |
| F |
F |
T |
T |
T |
典型的なトートロジーと呼ばれる変形である.
よく知られているように,→は,前件(条件部)がF(偽)ならば,後件の真偽にかかわらずT(真)である.前述のように,そういう規則と割り切っておかないといけない(なお,この点については再度触れることにする).
「Cの場合は,Aを実行します」と仕様書に書いてあったとする.¬Cの場合に,異常なふるまいをしたときに,それは仕様外ですといえるかどうかは,ケースバイケースである.プログラミングであれば,防衛的にすべきという標語が相当するか.
(nil)