我々のモデリングアプローチ,特にステートチャート言語は,反応型のシステムに有効である.そのふるまいは複雑で,よく知られているように,見つけにくい誤りに満ちた仕様上の問題を引き起こす.多くのリアルタイムシステムは,相当する 1
ステートチャートは,いまではよく知られている.しかし,OMT手法で取りあげられる前は,余り一般的ではなかった.また,ステートチャートの記法の全てが採用されているわけではない.
冒頭の文は,数少ないHarel氏の著作から引用してる 2.副題は,STATEMATEアプローチである.STATEMATEはツールの名前である.かつて私はSTATEMATEのユーザだった(動作環境は,SUN OS).
それで少し振り返る.STATEMATEを作っていた I-Logix社は,DOORSで有名だったTelelogic社に買収された.Telelogic社はRational社に買収され,現時点ではIBM社の1部門である.この食物連鎖のような移り変わりを見ているとツールビジネスの難しさを感じる.しかし,それでも残っているのは,オリジナルのアイデアが優れていたからに違いない.
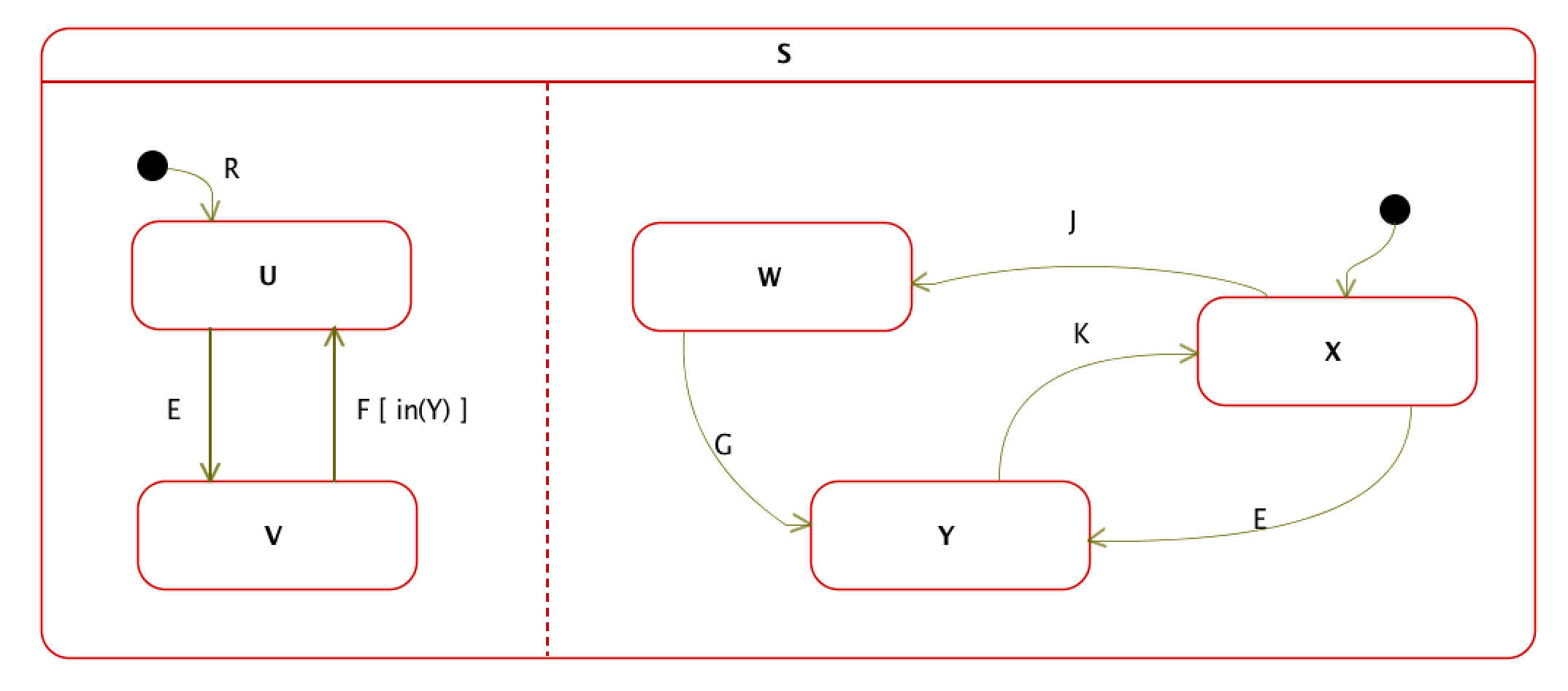
さて,ステートチャートには幾つもの特徴がある.もっとも代表的なものは直交表現である.
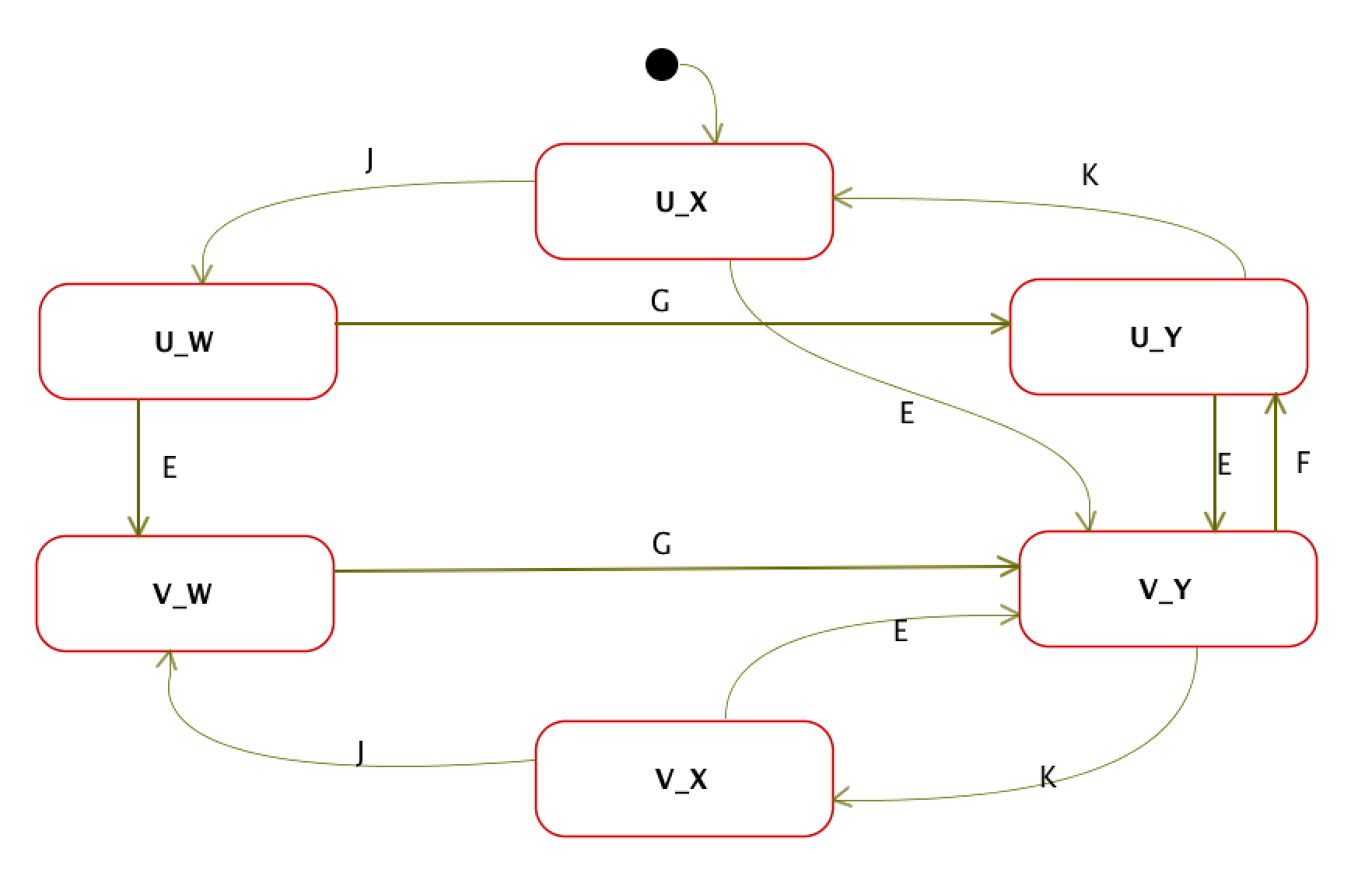
上記で,点線 3で仕切られた2つの状態遷移図は,並列に動作することを示している.上図と同値で,直交表現を使用しない状態遷移図だと以下になる.
如何に直交表現が端的に表現できるかが分かる.
例えば,初期状態(状態Uと状態X,非直交表現では,U_X)で,イベントEを受けたときには,状態Vと状態Y(非直交表現では,V_Y)に移動するが,見やすさは,直交表現が優る.
もちろん,2つ状態遷移図を並べて,両者は並行動作するといっても良いのだが,図式として説明を不要にしている.また,VからUへの遷移にでてくるF[in(Y)]は,「(隣の状態遷移図で)Yにいるならば,FイベントでUに遷移する」という意味になる.変数のスコープも含めて扱いが容易である.
ちなみに,「in(S)」キーワード は,「システムがS状態にいる」として,オリジナルのステートチャートでは定義されている.このほかにもタイムアウトやクロックなどの様々なキーワードが定義されている.その一部は,しばらくしたところで紹介があるので,ここでは省略する.
(nil)
Notes:
- David Harel and Michal Politi. Modeling Reactive Systems with Statecharts: The Statemate Approach (1st ed.). McGraw-Hill, Inc, 1998, p.3 ↩
- Harel氏は,Computers Ltd. what they really can’t doという小冊子だが見事な読みものも書いている ↩
- 点線自身をUMLでは,アンドラインと呼ぶ.しかし,STATEMATEでは,特別の呼び名はない.他の図式でもそうだが,実線のノードをまとめるときに点線を用いている.また,点線を含む状態のことを,「AND状態(AND state)」と呼んでいる. ↩