今回は，データフロー図である．
データフロー図では，入力データと出力データおよびその変換器ノードによって，全体を表現する．シンプルなモデルで，構造化分析が話題になっていた頃は，よく書かれていた．
シンプルさは，逆にいえば，難しさも伴う場合がある．どのような風にも自由に書けてしまう．一番の間違いは，変換器ノードを機能表現と見なしてしまうことによって生じる．変換器（手法によっては，プロセス）は，データの変換器である．データの変換は，もちろんなんらかの機能には違いない．ただし，あくまで，データとその変換に注目したときに，分かりやすい図とすることが重要である．
機能視点で分割してしまうと，データがあちこち分散する可能性があり，折角のデータ中心の整理が，出来なくなってしまう．
リアルタイム処理用には，Hatley方式とWard方式の2つの記述法が，その後生まれた．こちらは，制御およびその流れを記載するため，機能的視点でも問題はない．
Ward法教科書表紙
上記は，手持ちのWard法の教科書 の第一巻である（全3巻）．表紙は時代を感じる．しかし，内容は，今でも通用する．進歩しているようでしていないことに，気づく．
(nil)
SADT（Structured Analysis and Design Techinique）は，企業色があったせいか，日本では余り用いられなかった（もっとも，構造化分析・設計が騒がれたときも，実際に使っている人たちは少なかった）．
機械系の人には懐かしい図面風の図を作る．基本的な要素を，以下の図に示す．
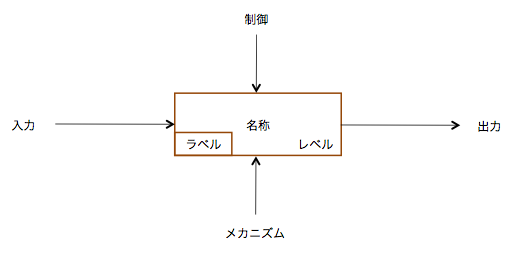
SADT基本ノード
入力と出力は，ごく一般的な書き方である．「ラベル」は，ノードの識別子となる．後述するアクティグラムとデータグラムは同じ書き方をするために，ラベルで区別する．例えば，アクティビティを表現するのであれば，Aから始まる識別子をつけ，データであれば，Dから始まる識別子をつける．レベルとあるのは，各ダイヤグラムの階層上のレベルである．構造化分析・設計と同様に，詳細化に従い，複数のダイヤグラムを記述する．そのレベルである．
さて，制御とメカニズムは何か？
SADTでは，2つの図を用いる．アクティグラム(Actigram)とデータグラム(Datagram)である．前者はアクティビティの説明用で，後者は，アクティグラムにでてくる入出力データの説明用である．
2種類の図と制御・メカニズムの関係
|
制御 |
メカニズム |
| アクティグラム |
ふるまいを変える |
アクティビティの実行者（人・コンピュータ） |
| データグラム |
データの内部状態を変える |
データを保持する機構 |
アクティビティとデータの関係を同じ構造で記載することができる．
90年代にソフトウェア開発プロセスのモデル化がなされたときに，SADTを使って記述したことがある．プロセスはアクティビティの集合であり，記述が容易であった記憶がある．もちろん，プロセスのモデル化は，例外の多さに難しさがあり，図が書きやすいからといって解決はしないのが残念である．
（nil）
実体関連モデルと呼ぶデータモデルを提案する．実世界における重要な意味情報を組み込んでいる．
今回は，実体−関連（ER）図の説明である．いまでもビジネス系（特にデータベース設計）では良く用いられる．
その名の通り，実体とその関係が中心に記述する．実体は属性を持つことが出来る．単純には，実体はデータベース設計におけるテーブルに相当する．属性はカラムに対応する．
以下で，原書にある会議スケジュール管理システムの例を示す．この例では，ほとんどクラス図と同等の記載方法になっている（一部，表現を変更した）．
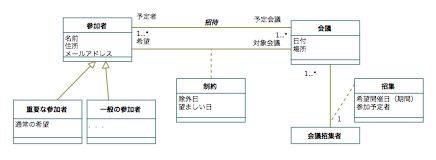
会議スケジュール管理システムの実体関連図
継承（サブクラスと書きたいが，対象は実体であり，サブ実体という用語はないので継承としておく）により，重要な参加者と一般の参加者を区別している（重要な参加者は，全員のスケジュールが合わないときに優先される）．2つの三項関係があり，関連クラスによって示される．
実体関連図は，実体とそれを繋ぐ関連図というよりは，関連とその両端にある実体の図といった方が正しい．上記の右側にある三項関係を，実体関連図の伝統的な記法で書くと下記のようになる（伝統的と云うのは，冒頭の文を含む論文は，今から40年ほど前に発表されているからである）．
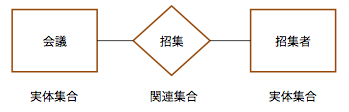
伝統的な実体ー関連図の記法
関連は，なんらかの働きを行う．実体は，その働きに対してなんらかの役割を果たす．当初のChen氏の論文では，そう考えることで現実世界を理解することができる，としていた．
もう一つのポイントは，矩形や菱形は，それぞれ集合となっている点である．クラス図に慣れてしまうと，クラス基準で考えたくなるが，あくまで，インスタンスで考える．クラスに相当するものは集合として捉える．
クラスで考えることと，インスタンスで考えることは，最終的には同じように思うが，できあがったモデルに違いが現れる場合が多い．全体は，クラスで考える方が考えやすいが，細部では，インスタンスで考える方が考えやすく，思い込みによる間違いを減らすことができる．
実体ー関連図は，継承を取り込むことで，以前は，拡張実体ー関連図（EER）と呼ばれた．それは，図式としては現在のクラス図に近い．しかし，クラス図となると，当初のの実体ー関連図で，考えられていたこととは違った考え方で用いられる場合も多い．
もちろん，結局のところ，「図に，良し悪しはない．役立つか立たないかだけだ」
（nil）