三章（要求の評価）のまとめである．
最初は，要求文中の衝突をどう回避するかの議論であった．そのために，問題解決を考えたり，代替策を考える．プロセスとしては，リスク分析およびより広いリスク管理の議論へと進んだ．最後は，リスク管理を体系的に（定量的に行うための）方法のひとつとしてのAHPを紹介している．
本書にもあるとおり，なぜこのステップがあるかである．2章は，要求抽出であり，ここでの議論は，そのまま前章に利用することができる．しかし，最終的な要求は，自動的に導出されるものではない以上，当事者たる利害関係者だけで定まるのか ? という疑問がある．結局は，声の大きい人が勝つかもしれない．
本章では，リスクの導出法や，代替策の評価について，幾つかの体系的な方法が示されている．それらに対して，正しく利害関係者が認識していれば，より合理的に要求を評価できるに違いない．
上記は，欧州的な考え方なのかもしれない．利害関係者同士が納得出来るにように，合意し要求を作るというのは，理念的ですばらしい．現実には難しいし時間も掛かるが，欧州の人たちはそれを目指しているように思う．少なくとも理念としては持つ．現実は違うかもしれないが，聞かれればそう答えるに違いない．
日本のどこかの会議で，「チームは，要求を素早く見つけ共有しなければならない」という話をしていた人に，質問したことがある．その要求は誰の要求かと．
「みんなが共有するのは，お客さんの要求に決まっている．それ以外に何があるのか．」という答えで，少しうろたえたことがある．異なる世界は，そもそも存在していない．彼にとって要求はお客さんから頂くものでしかない．
理念的かもしれないが互いの要求をシェア・調整しようと考えるのと，特定の利害関係者を尊重するのとどちらが良いか．個人としては，前者の世界が過ごしやすい．
（nil）
さて，前回は，手計算で重みとCIを手計算で行った．実際に手計算することはないと思うが，一度だけなら楽しい．
さて，前回のペア比較は，ソフトを改修した場合の効果についてのものだったとする．代替案A＞代替案C＞代替案Bの順番であったから，代替案Aが最も効果的ということになる．次は費用に関して同様に計算してみる（今回は手計算しない）．
簡単なペア比較表（費用）
|
代替案A |
代替案B |
代替案C |
| 代替案A |
1 |
1/4 |
1/5 |
| 代替案B |
4 |
1 |
1/2 |
| 代替案C |
5 |
2 |
1 |
重みベクトルとCIは，次になる．
t ， CI = 0.012
CIは，0.1より小さいので有効である．さて，費用から見た場合の代替案の重要度は，代替案C＞代替案B＞代替案Aとなる．これは，効果から見た場合の優先度とは異なっている．最終的に，どのような優先度とすべきか．
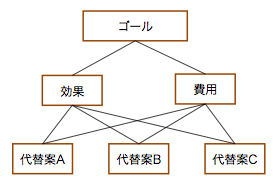
AHPの階層構造
AHPは，その名前の通り階層構造をとる．ゴールをレベル１，効果と費用をレベル２，各代替案をレベル３とすると，レベル２とレベル３の間の重み付けは既に計算している．以下の結果であった（ここでは，有効桁数を増やした結果を示す）．
t
次に，レベル１とレベル２の間の重み付けを考える．これまでと同様に，ペア比較表を作る．
簡単なペア比較表（レベル１-２）
|
効果 |
費用 |
| 効果 |
1 |
1/5 |
| 費用 |
5 |
1 |
いまは，とにかく費用を重視したいとする．ここから計算する重み付けは，以下になる．
t
最終的な，重み付けは，それぞれの積和をとることで計算できる．費用対効果を勘案した，代替案の重みは，次になる．
代替案A：0.167 * 0.743 （効果分）＋ 0.833 * 0.097 （費用分）= 0.205
代替案B：0.167 * 0.063 （効果分）＋ 0.833 * 0.333 （費用分）= 0.288
代替案C：0.167 * 0.194 （効果分）＋ 0.833 * 0.570 （費用分）= 0.507
従って，最終的な代替案の評価は，代替案C＞代替案B＞代替案Aとなる．「効果」に比べ，今回は「費用」をかなり重視したので，費用単独の順位と同じになっている．ちなみに，KAOSの教科書では，効果と費用は同一の重みで比較している．
さて，AHPについて，少し詳しく見てきた．少し前のAHPの本 では，様々なヴァリエーションの説明がある．相対的な評価ではなく絶対的な評価を行うもの，必ずしも独立性を前提としないものなどである．構造も単純な木構造ではなく，ネットワーク型となるものもある．
何度かこの項で説明しているように，ある種の合理的な説明は，これからも必要だろうと思う．そのときに，（最も基本的なモデルにおいても）AHPは，良い計算手段を提供している．
（nil）
今回は，手計算で，前回のペア比較表から，各代替案の重みと整合性指標を求める．
簡単なペア比較表
|
代替案A |
代替案B |
代替案C |
| 代替案A |
1 |
9 |
5 |
| 代替案B |
1/9 |
1 |
1/4 |
| 代替案C |
1/5 |
4 |
1 |
| 列の合計 |
1.311 |
14 |
6.25 |
前回と同じであるが，列の合計値を加えている．
この合計値を用いて，各列を正規化する．
正規化した結果
|
代替案A |
代替案B |
代替案C |
| 代替案A |
0.763 |
0.643 |
0.800 |
| 代替案B |
0.085 |
0.071 |
0.040 |
| 代替案C |
0.152 |
0.286 |
0.160 |
| 列の合計 |
1.000 |
1.000 |
1.000 |
次に，行毎の平均をとり，重みベクトルとする．
正規化した結果に対して行の平均を求める
|
代替案A |
代替案B |
代替案C |
平均 |
| 代替案A |
0.763 |
0.643 |
0.800 |
0.735 |
| 代替案B |
0.085 |
0.071 |
0.040 |
0.065 |
| 代替案C |
0.152 |
0.286 |
0.160 |
0.199 |
| 列の合計 |
1.000 |
1.000 |
1.000 |
0.999 |
重みベクトルは，tになる（丸め誤差で，合計が１ではない．tは転置行列であることを示している）．最初のペア比較表に，この重みを掛け合わせる．主たる目的はここで達成している．次は，そもそも妥当な入力を最初にしたかの確認用である．
重みを掛けたペア比較表
|
代替案A |
代替案B |
代替案C |
行の合計 |
合計／重み |
| 代替案A |
0.735 |
0.585 |
0.995 |
2.315 |
3.150 |
| 代替案B |
0.082 |
0.065 |
0.050 |
0.197 |
3.031 |
| 代替案C |
0.147 |
0.260 |
0.199 |
0.606 |
3.045 |
ここで「合計／重み」の平均値を計算すると，3.08が得られる．これで，表計算は終了である．大学に入った最初の線形代数演習を，いつも思い出してしまう．
この3.08が，ペア比較マトリクスの最大固有値（λmax）になる（有効桁数を4桁以上とると，3.07127となる．ただ入力値が実験結果というわけではないので，細かな違いを気にしても仕方がない）．
ここから，整合度指数（Consistency Index，CI）を計算する．計算式は，次である．
CI = (λmax – n)/(n – 1)
有効桁数値を増やした値を用いて計算すると，CIは，0.0357となる．通常は，この値が，0.1より小さければ，ペア比較マトリクスは妥当とする．
さて，まとめる．今回の計算で重要なのは，重みベクトルである．重みベクトルは，最終的な代替案の重要性を示している．ここでは，t であり，優先度は，代替案A＞代替案C＞代替案Bとなる．
もう一つは，最後に計算したCI値である．前回見たようにペア比較するときに，全体の表をイメージしてしまうと，ペアでの比較ではなくなる．そこで整合性をあえてとるような入力をすると，CIはゼロになってしまう（実際には，入力可能な値に限りがあります）．或いは，一貫性を持たない入力をすると，大きな値になる．
閾値0.1は，経験値である．しかし，不真面目な入力をチェックするのに役立つ．特に，アンケートでは．
（この項つづく）
（nil）