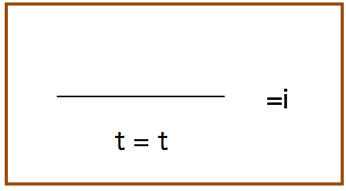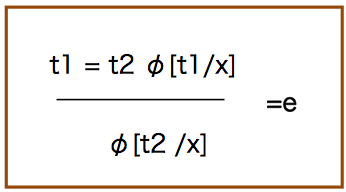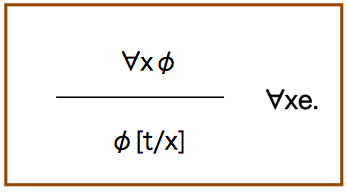さて,今回は述語論理における推論(証明)規則である.
最初の規則である.
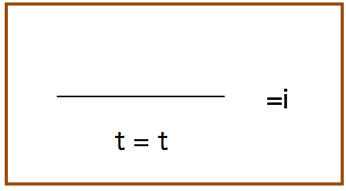
入-=
これは,当たり前で,かつ余り役に立たない.次は,等号に関する削除の規則である.
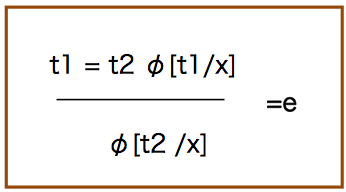
去-=
いま,xがΦの束縛変数とする.明らかにt1, t2 は自由変数となる.t1 と t2 は等しいので,Φ[t2/x]と結論づけることができる.少し具体的な例を見てみる.それぞれ論理式は以下だとする.
t1: (x+1)
t2: (1+x)
Φx:((x>1)→(x>0))
論理式Φ[t1/x] は,((x+1)>1)→((x+1)>0)である(t1/xは置き換えを表す).いま,t2に変えた論理式 ((1+x)>1)→((1+x)>0)も正しいことがわかる.
さて,このどこが述語論理式の推論規則かと思ってしまうが,次につながる.
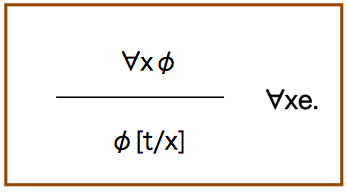
instantiation
インスタンス化(instantiation)と呼ばれる述語論理の推論規則を得ることができる.
前提が示すところは,全ての束縛変数xに関してΦは成立している.だとすると,例えば定項としてt(変項xの一つの値)をいれた場合でも成立しなくてはならない.
ずいぶんと後退しているようであるが,全称限量子を外せる効果は大きい.
(nil)
今回は,練習を兼ねて,限量子での同値の関係にある変形を見てみる.
「とべないトリがいる」は,述語「トリである」をB,述語「とべる」をFとすると,次の様に書ける.
∃x(B(x)∧¬F(x))
これは,「全てのトリがとべるわけではない」ということと同じと考えると,次の様にも書ける.
¬∀x (B(x) → F(x))
この式を変形してみる.B(x)→F(x)は,以前に命題論理のときに操作したように,¬B(x) ∨ F(x)と書ける.¬∀xP(x)が∃x(¬P(x))と書くことができれば,¬(¬B(x) ∨ F(x))は,B(x)∧¬F(x)なので,最初と同じになる.
¬∀xP(x)が∃x(¬P(x))は,ここでは,明らかであるということにしておく(次回の全称量子化の置き換え・インスタンス化を使用する).
さて,幾つかの定理を並べる.
なお,「⊣⊢」の意味は, φ1 ⊢ φ2 であり,かつ φ2 ⊢ φ1という定理を示している.これらの規則は背理法を用いて示すことができる.最後に,限量子の除去に関して,簡単に説明する.前半部分は,おそらく明らかであろう.なお,「束縛」と「限量子の除去」において,ψは,xを項として持つ.
幾つかの規則(定理)
| 否定 |
|
|
|
| 束縛 |
|
|
|
|
|
|
|
| 限量子の除去 |
|
|
|
|
|
|
|
| 束縛範囲 |
|
∃x φ ∨ ∃x ψ ⊣⊢ ∃x (φ ∨ ψ)
|
| 束縛順 |
|
|
|
∀x(ψ→φ)⊣⊢ψ→∀xφを説明する.
最初は,∀x(ψ→φ) ⊢ ψ→∀xφ から.
結論を否定すると,¬(ψ→∀xφ).これは,ψ ∧ ¬∀xφと同じ.
ψも¬∀xφもともに真でなくてはならない.即ち,∃x¬φ(表の一番上の規則)
前提で,ψが真の場合,φはつねに真でなくてはならない.これは,偽の場合もあるという∃x¬φと矛盾するので,背理法から∀x(ψ→φ) ⊢ ψ→∀xφがいえる.
次にψ→∀xφ⊢∀x(ψ→φ) を示す.結論を否定して仮定を作る.∃x¬(ψ→φ)(表の一番上の規則から).これは,∃x(ψ ∧¬φ)と変形できる.つまり,ψが真,φが偽になる組が存在する.ところが,前提は,ψ→∀xφであるから,ψが真であれば,常にφは真である必要がある.従って仮定と矛盾するので,背理法からψ→∀xφ⊢∀x(ψ→φ) がいえる.
(nil)
記号論理自体は,それ自体で閉じた世界である.
それを利用するとなれば,我々が住んでいる現実世界と紐づける必要がある.紐付けることで,始めて要求を管理するという目的に役立つことになる.
さて,述語論理に戻る.今回は,もう一つの述語論理の特徴である限量子(量化子)についてである.
限量子
| 種類 |
記号 |
文での使用例 |
| 全称限量子 |
∀xP(x) |
全てのxで,P(x)である |
| 存在限量子 |
∃xP(x) |
あるxで,P(x)である |
限量子とともに用いるxのことを束縛変項と呼ぶ.「”あるxにおいて”Pxが成り立つ」といっているのであるから,xは,「ある(∃)」によって束縛されている.束縛されていない変項のことを,自由変項と呼ぶ.
さて,例題に用いている列車の運行管理システムの例は,次のように記述できる.
∀tr1, tr2(Following(tr2, tr1) → Dist(tr2, tr1) > WCS-DIST(tr2))
tr1,tr2は,束縛変数である.∀xP(x)→Q(x)というときに,限量子は,P(x)のxのみを束縛する.∀x(P(x)→Q(x))ならば,Q(x)のxも束縛されている.
参考までに,文の解釈を示しておく.
全ての列車に関して次が成立する.いま,tr1, tr2 と名前をつけ,tr2は,tr1の後ろを走っているとする.このときに,tr2とtr1の距離は,tr2の最悪時近接距離より大きくなければならない.
「全て」であるから命題論理でも同じように書くことができる.しかし,述語を使うことによって,文の構造が分かりやすくなる.また,複数の変項を持つことにより,表現できることが増える.
(nil)